Cowdery Numbers
Background
I have discovered (during my A level maths classes instead of listening to the teacher!) a series of number pairs, the reciprocals of which contain the same digits after the decimal point as the other number in the pair. I discovered these by firstly noting that sqrt(2)+1 had the same bits after the decimal point as 1/(sqrt(2)+1). Random calculator fiddling showed that this property wasn't a unique result.
For example,
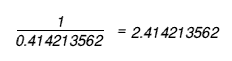
And similarly:
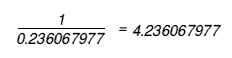
and
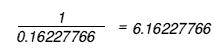
Theory
A general formula for generating the numbers is as follows:

Where n is any integer (or an integer + 0.5 - see proof B).
Proof A
- Proof that the reciprocal of one number is the other
Equate the two numbers
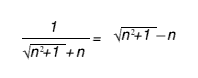
Cross multiply
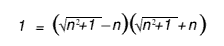
Multiply out
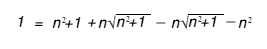
Simplify
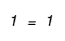
QED!
Proof B
- Proof that the two numbers are identical after the decimal point for an infinite number of decimal places
To prove this, simply show that the difference between the two numbers is an integer. This can be shown by subtracting the two numbers:

The difference between the two numbers is 2n, and since n is an integer, so is 2n, and thus the two numbers in the Cowdery pair are indeed identical to an infinite number of decimal places. It follows that as 2n must be an integer, n can be an integer + 0.5 and the theory holds.
The real proof
The real proof is of course:
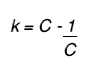
What is the set of C for which k is an integer.
Rearranging into standard quadratic form:
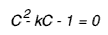
Which can be solved using the standard formula for quadratics where a=1, b=-k and c=-1. This gives C in terms of k:

Which is the same as the equations shown above.
And this gives the results shown in the table below:
Results
Here are the first 21 Cowdery Number pairs:
| Cowdery Number (n) | < 1 | > 1 |
|---|---|---|
| 0.5 | 0.6180339889 | 1.6180339889 |
| 1 | 0.4142135624 | 2.4142135624 |
| 1.5 | 0.3027756377 | 3.3027756377 |
| 2 | 0.2360679777 | 4.2360679777 |
| 2.5 | 0.1925824033 | 5.1925824033 |
| 3 | 0.1622776603 | 6.1622776603 |
| 3.5 | 0.1400549449 | 7.1400549449 |
| 4 | 0.1231056247 | 8.1231056247 |
| 4.5 | 0.1097722296 | 9.1097722296 |
| 5 | 0.0990195144 | 10.0990195144 |
| 5.5 | 0.09016994387 | 11.09016994387 |
| 6 | 0.08276253007 | 12.08276253007 |
| 6.5 | 0.07647321932 | 13.07647321932 |
| 7 | 0.07106781192 | 14.07106781192 |
| 7.5 | 0.06637297571 | 15.06637297571 |
| 8 | 0.0622577481 | 16.0622577481 |
| 8.5 | 0.0586213842 | 17.0586213842 |
| 9 | 0.05538513884 | 18.05538513884 |
| 9.5 | 0.05248658732 | 19.05248658732 |
| 10 | 0.04987562075 | 20.04987562075 |
Of course the keen eyed amongst you will have observed that the Cowdery number for n=0.5 is the Golden Ratio, known to the ancient Greeks.
Questions:
Are these numbers already known about?
Do they have any use?
